Lorenzkurven

Lorenzkurven visualisieren Ungleichheiten etwa bei der Einkommensverteilung

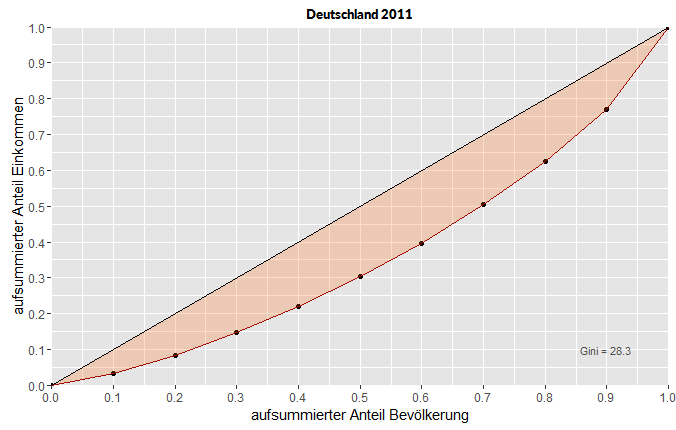
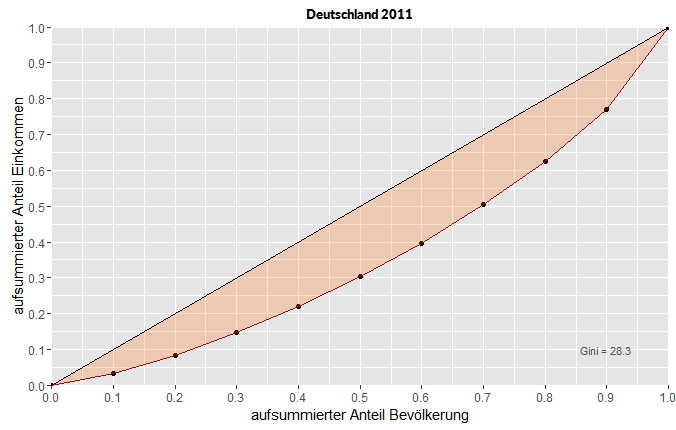
Lorenzkurven sind eine grafische Darstellungsform für die Abbildung von Ungleichheit und werden typischerweise für Einkommensverteilungen verwendet. Eingeführt hat sie Max Otto Lorenz im Jahr 1905. Das Beispiel zeigt die Lorenzkurve der Einkommensverteilung in Deutschland im Jahr 2011.
Eine perfekte Gleichverteilung würde in dem Plot einer Linie im Winkel von 45 Grad entsprechen. Die Lorenzkurve zeigt dabei grafisch, wie weit die Realität von der Idealvorstellung abweicht. Neben der grafischen Darstellung stellt auch der Gini-Koeffizient ein Maß der Abweichung dar. Ein Gini-Wert von 0 beduetet perfekte Gleichverteilung, und ein Wert von 100 drückt eine perfekte Ungleichverteilung aus. Die Daten kommen von der Seite www.wider.unu.edu./research/Database/ und werden in Form einer Excel-Tabelle in das Skript geladen.

library(gdata)
library(ggplot2)
library(extrafont)
library(ineq)

daten <- read.xls("daten/einkommen.xlsx",head=T,skip=1,dec=".")
G <- rep(10,10)
G_kum <- c(0,cumsum(G/100))
G1 <- daten$G1
G1_kum <- c(0,cumsum(daten$G1/100))
D1 <- Lc(G1, n = rep(1,length(G1)), plot = FALSE)
p <- D1[1]
L <- D1[2]
D1_df <- data.frame(p,L)
xx <- c(G_kum,rev(G_kum))
yy <- c(G1_kum,rev(G_kum))
koordinaten <- as.data.frame(xx)
koordinaten$yy <- yy
gini <- round(ineq(G1) * 100, digits = 1)

p1 <- ggplot(data=D1_df) +
  geom_point(aes(x=p, y=L)) +
  geom_line(aes(x=p, y=L), stat = "identity", color="#990000") +
  scale_x_continuous(name="aufsummierter Anteil Bevölkerung", limits=c(0,1), breaks = seq(0, 1, 0.1), expand = c(0, 0)) + 
  scale_y_continuous(name="aufsummierter Anteil Einkommen", limits=c(0,1), breaks = seq(0, 1, 0.1), expand = c(0, 0)) +
  ggtitle("Deutschland 2011") + 
  theme(plot.title = element_text(size=10, hjust=0.5, family="Lato Black"),
        panel.background = element_rect(fill = "grey90", colour = "grey95")) + 
  geom_polygon(data = koordinaten, aes(x = xx, y = yy), fill = rgb(255,100,0,55,maxColorValue=255)) +
  annotate("text", x = 0.9, y = 0.1, label = paste("Gini =", gini), size=3, colour="gray30") +
  geom_abline()
p1

Das Skript: Das Skript lädt zunächst die benötigten libraries, das ist gdata, um Excel-Tabellen zu importieren, ggplot2 für den Plot, und ineq für die Berechnung des Gini-Indexes. extrafont ist optional. Es folgt das Einlesen der Excel-Tabelle mit Hilfe von read.xls(). Der folgende Block berechnet den Gini-Index und erstellt einen Data Frame und die Koordinaten für die Lorenzkurve. Letztere wird im Plot als Polygon eingezeichnet.
Der nächste Block konstruiert den Plot mit ggplot(). geom_point() zeichnet in 10-Prozent-Schritten die tatsächlichen Werte ein. geom_line() verbindet die Punkte mit einer Linie. geom_polygon() schließlich generiert die Lorenzkurve und färbt sie entsprechend ein. geom_abline() erstellt die 45-Grad-Linie, die einer optimalen Gleichverteilung entspräche. Der Gini-Index wird mit annotate() hinzugefügt. Alles übrige ist kosmetischer Natur.
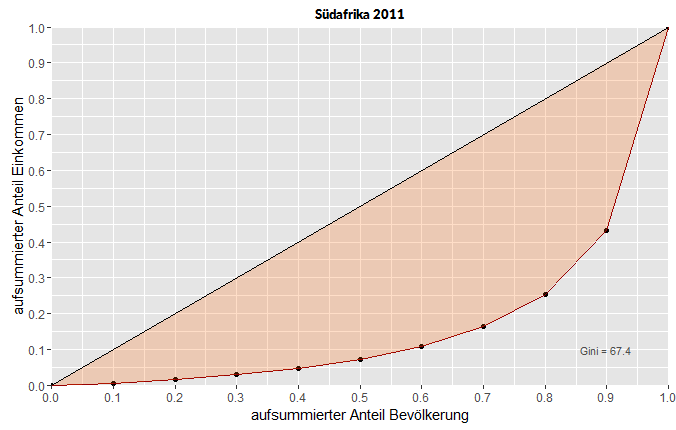
Deutschland steht bei der Einkommensverteilung ganz gut da, was auch der Gini-Wert von 28,3 dokumentiert. Die farbige Fläche der Lorenzkurve ist recht klein. Die unteren 60 Prozent haben immerhin etwa 40 Prozent des verfügbaren Einkommens. Ganz anders sieht es etwa in Südafrika aus. Hier beträgt der Gini-Index 67,4 und die Fläche der Lorenzkurve ist ziemlich groß. Die unteren 60 Prozent der Bevölkerung erhalten nur rund 10 Prozent des verfügbaren Einkommens, während die oberen 10 Prozent über 55 Prozent des Einkommens verfügen.