Erste Schritte mit Mathematica und der Wolfram Language
Mathematica hat seine Wurzeln in der Mathematik, geht aber inzwischen weit darüber hinaus. Es ist ein Füllhorn von Daten und Wissen mit schier unerschöpflichen Möglichkeiten.
Die zugrunde liegende Programmiersprache nennt sich Wolfram Language [1], denn der Erfinder Stephen Wolfram ist ziemlich eitel. Mathematica 1.0 ist bereits 1988 auf den Markt erschienen. Wolfram Language ist eine wissensbasierte symbolische Programmiersprache. Sie verfügt über unzählige eingebaute Funktionen, Algorithmen und Wissensdatenbanken und unterstützt mehrere Programmier-Paradigmen wie die funktionale, symbolische und regelbasierte Programmierung.
Mathematica ist recht teuer und schlägt normalerweise mit mindestens 400 Euro zu Buche. Aber Wolfram Research spendiert jedem Raspberry Pi ein für private Zwecke kostenloses Mathematica [2]. Im Betriebssystem Raspberry Pi OS ist es bereits standardmäßig installiert. Ansonsten lässt es sich im Terminal mit dem Befehl sudo apt install wolfram-engine nachinstallieren. Die Stand August 2021 aktuelle Mathematica-Version ist 12.3.1. Die Version 12.2 auf dem Raspberry Pi ist nicht brandaktuell, aber ziemlich nahe dran.
Wolfram gibt die Zahl der Datenpunkte in der Knowledge Base [3] mit knapp 10 Billionen an. Zur Veranschaulichung: Das ist etwa die Zahl an Kilometern, die Licht in einem Jahr zurücklegt.
Prinzipen von Mathematica
Um Mathematica zu starten, rufen Sie im Startmenü im Abschnitt „Entwicklung“ den Eintrag „Mathematica“ auf. Mathematica arbeitet Notebook- und Cloud-basiert und kann online auf eine enorm umfangreiche Wissens-Datenbank zurückgreifen. Eine Internetverbindung während der Nutzung erscheint also sinnvoll. In einem Notebook evaluieren Sie eine Eingabe und erhalten eine Ausgabe. Dann erfolgt die nächste Eingabe und so weiter.
Mathematica unterscheidet zwischen Groß- und Kleinschreibung. Funktionen werden grundsätzlich großgeschrieben. Bei zusammengesetzten Funktionen wie ListPlot gilt die Großschreibung für alle Bestandteile. Nach der Eingabe eines Befehls erscheint darunter eine kurze deutsche Erklärung dafür. Funktionen erfordern immer eckige Klammern, etwa Factorial[100], um 100! auszurechnen. Präzision und Genauigkeit sind beliebig groß.
Unter Listen ist bei Mathematica alles gemeint, was aus mehr als einem Element besteht. Das können etwa Zahlen, Wörter oder andere Listen sein. Listen sind von geschweiften Klammern umgeben. Eine Beispiel wäre die Liste {1, 4, 9, 16, 25, 36, 49, 64}. Um einen Befehl auszuführen – oder wie es bei Mathematica heißt zu evaluieren –, drücken Sie die Tastenkombination [Umschalt]+[Eingabe] oder Sie verwenden die Eingabetaste auf dem Zahlenblock Ihrer Tastatur. Um den vorherigen Input zu wiederholen, etwa um einen Parameter zu verändern, dient [Ctrl]+[L].
Vorarbeiten durchführen
Wolfram Research ist ein amerikanischen Unternehmen, das auf deutsche Tastaturlayouts keine Rücksicht nimmt. Die wichtige Tastenkombination [Ctrl]+[=] ist mit deutschen Tastaturen schlichtweg nicht machbar. Ein Weg aus der Misere besteht darin, einen Alias dafür festzulegen. Da Sie dazu Root-Rechte benötigen, öffnen Sie im Terminal mit sudo geany einen Texteditor. Dann navigieren Sie in das Verzeichnis „/opt/Wolfram/WolframEngine/12.2/SystemFiles/FrontEnd/TextResources/X“. Dort öffnen Sie die Datei „MenuSetup.tr“. Suchen Sie die Zeile mit dem Inhalt MenuItem["Inline Free-form Input",. Ändern Sie in der eingerückten übernächsten Zeile MenuKey["=", Modifiers->{"Control"}] ab in MenuKey["F9", Modifiers->{}] und speichern Sie die Datei. Nach einem Neustart des Programms ersetzt fortan F9 die unmögliche Tastenkombination.
Nicht zwingend notwendig, aber sinnvoll ist der Schritt, das Notebook-Verzeichnis zu den vertrauenswürdigen Verzeichnissen hinzuzufügen, um ständige Warnmeldungen zu vermeiden. Dazu rufen Sie in Mathematica den Menüpunkt „Edit“, „Preferences…“ auf und wechseln dann zum Reiter „Security“. Ein Klick auf „Edit Trusted Directories…“ führt zu einem neuen Fenster. Hier geben Sie nach einem Klick auf „Add“ das Verzeichnis „/home/pi/Documents/Wolfram Mathematica“ ein und bestätigen das Ganze zwei Mal mit „OK“.
Erste Schritte mit Mathematica
Mathematica läuft auf dem Zwerg-Rechner bei Weitem nicht so flott wie auf einem ausgewachsenen PC, aber zumindest mit einem Raspberry Pi 4 ist es erträglich. Nach dem Start von Mathematica erscheint automatisch ein neues Notebook, das Sie später mit [Strg]+[S] oder über das Menü speichern können.
Im einfachsten Fall lässt sich Mathematica als äußerst leistungsfähiger Taschenrechner nutzen. Geben Sie etwa 4596 + 8773 * 8787 ein und evaluieren Sie die Zelle mit [Umschalt]+[Eingabe]. Mathematica beachtet alle mathematischen Grundregeln wie „Punkt vor Strich“. Das Ergebnis von (4596 + 8773) * 8787 ist somit ein anderes. 12^144 berechnet 12 hoch 144 und 718 / 3 hat einen Bruch als Ergebnis. Um stattdessen einen numerischen Zahlenwert zu erhalten, dient die Funktion N. Sie lässt sich auf zwei Arten anwenden: N[718 / 3] oder 718 / 3 //N.
Free-form Input verwenden
Die Verwendung von Mathematica als Taschenrechner ist so, als würde man eine Ferrari nur im ersten Gang fahren. Das Programm kann so viel mehr. Das folgende Beispiel zeigt eine der Stärken, die Nutzung von Entitäten. Entitäten sind alle möglichen Arten von Dingen, über die Mathematica alles Mögliche weiß. Sie stammen aus der Wolfram Knowledge Base. Der einfachste Weg, auf diese Daten zuzugreifen, ist einfaches Englisch. F9 teilt Mathematica mit, dass Klartext folgt. Das nennt sich Free-form Input.
Wenn man F9 drückt, dann erscheint ein Eingabefeld mit einem Ist-Gleich-Zeichen davor. Geben Sie in das Feld etwa Italy ein und evaluieren die Zelle. Mathematica teilt mit, dass es die Eingabe als Land erkannt hat. Eigenschaften werden in eckigen Klammern an die Entität angehängt. Wiederholen Sie die vorherige Eingabe, ergänzt um ["Flag"]. Das Ergebnis ist eine italienische Fahne. Um zu sehen, welche Eigenschaften mit Ländern verbunden sind, evaluieren Sie den Code EntityValue["Country", "Properties"]. Sie erhalten eine sehr lange Liste.
Die nachfolgenden Abschnitte sollen zeigen, was in Mathematica steckt, und beispielhaft zeigen, welche Wissensbereiche sich damit abdecken lassen.
Geografie: Karten und Modelle
Öffnen Sie mit F9 ein Feld für Free-form Input, und geben Sie dort Mount Everest ein. Mit einem nachgestellten ["Elevation"] erhält man die Höhe des höchsten Berges der Erde. Das ist gleichbedeutend mit Entity["Mountain", "MountEverest"]["Elevation",] und lässt sich mit jedem Berg der Erde wiederholen. Eine andere Form der Eingabe ohne Free-form Input erfolgt in der Art = elevation of fuji. Das ist noch nicht sonderlich beeindruckend. Ein Reliefplot des Mount Everest legt da schon eine Schippe drauf. Der Code dazu sieht so aus:
ReliefPlot[ GeoElevationData[GeoDisk[Entity["Mountain", "MountEverest"], Quantity[10, "Kilometers"]]]]
Der Code funktioniert natürlich auch mit allen anderen Bergen wie dem Fuji oder dem K2. Wenn Sie einen leistungsfähigen Raspberry Pi besitzen, dann lässt sich eine dreidimensionale, frei drehbare Darstellung der Himalaya-Region erstellen mit
ListPlot3D[ GeoElevationData[GeoDisk[Entity["Mountain", "MountEverest"], Quantity[5, "Kilometers"]]], MeshStyle -> None]
Das bringt den Mini-Rechner an seine Grenzen. Deshalb machen wir mit etwas Einfacherem weiter. Um die Entfernung zwischen zwei Städten zu ermitteln, verwendet man etwa GeoDistance[F9Hamburg, F9Munich]. Die Namen der Städte sind dabei als Free-form Input einzugeben, also mit der Taste F9. Das Ergebnis 592 Kilometer bedeutet Luftlinie. Um die Reisedistanz mit dem Auto zu bestimmen, verwendet man TravelDistance[F9Hamburg, F9Munich]. Das ist mit 773 Kilometern schon deutlich weiter.
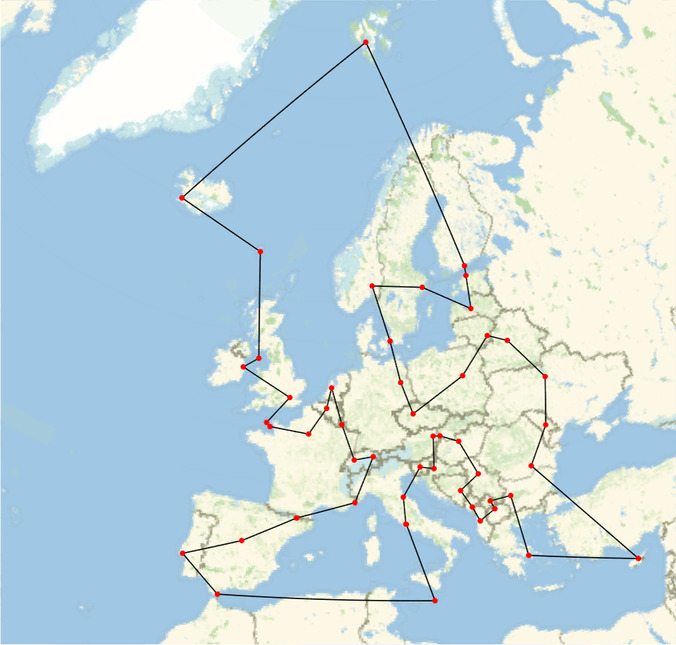
Das Problem, die kürzeste Entfernung zwischen mehreren Punkte zu bestimmen, heißt auch Travelling Salesman Problem. Wer einen langen Urlaub plant mit dem Ziel, alle europäischen Hauptstädte zu besuchen, kann sich vom Mathematica die kürzeste Route ausspucken lassen, indem er nacheinander die folgenden vier Befehle ausführt.
capitals = EntityClass["Country", "Europe"]["CapitalCity"]
GeoPosition[capital]
{d, perm} = FindShortestTour[%]
GeoGraphics[{GeoPath[capitals[[perm]]], Red, PointSize[Medium],
Point[capitals]}]
Hier zeigt sich ein Bug von Mathematica 12.2 auf dem Raspberry Pi. Die Hintergrundkarte erscheint erst, wenn man ein paar Mal mit dem linken oder rechten Mauszeiger in das Bild klickt. Über das Kontextmenü lässt sich die Grafik exportieren und ausdrucken.
Astronomie: Planeten und Monde
In Sachen Astronomie ist es zunächst einmal naheliegend, die acht Planeten des Sonnensystems darzustellen. Das erledigt F9planets["Image"]. Zur Erinnerung: Dazu klicken Sie F9, geben in das Feld planets ein und hängen [„Image“] an. Die Ausgabe besteht aus acht Bildern der Planeten unseres Sonnensystems. Wenn Sie der Meinung sind, dass Pluto Unrecht geschieht, dann holen Sie sein Bild mit F9Pluto["Image"] in das Notebook.
Um den Durchmesser der Planeten zu veranschaulichen, gibt man BarChart[EntityValue[F9Planet,"Diameter"]] ein. Um das gleiche mit der Masse darzustellen, verwendet man BarChart[F9Planet,["Mass"]]. Die Masse der inneren Planeten ist im Vergleich zu den Gasriesen so klein, dass sie im Diagramm kaum zu erkennen ist. Als Tabelle lassen sich die Werte mit Text[Grid[PlanetData[PlanetData[], {"Name", "Mass"}]]] ausgeben.
Um 63 Monde des Jupiter namentlich kennenzulernen, liefert Mathematica mit AstronomicalData["Jupiter", "Satellites"] die entsprechenden Informationen. Bilder der Monde lassen sich nach dem Schema PlanetaryMoonData["Phobos", "Image"] anzeigen.

Meteorologie: Niederschlag und Temperaturen
Mit Mathematica lassen sich nicht nur aktuelle Wetterdaten wie Temperatur, Luftdruck und Niederschlag ermitteln, sondern auch historische. Die aktuelle Temperatur in München liefert WeatherData["Munich", "Temperature"]. Auf ähnliche Weise lassen sich etwa Luftdruck, Luftfeuchtigkeit, Wolkenbedeckung und Windstärke ermitteln. WeatherData["Properties"] zeigt eine Liste aller möglichen Messwerte. Wenn die Stadt einmal nicht erkannt wird, dann hilft der ICAO-Code eines nahegelegenen Flughafens [4]: DateListPlot[WeatherData["EDDM", "Pressure", {2021, 6}], Joined -> True] zeigt den Luftdruck für den Juni 2021 am Flughafen Franz Joseph Strauß.
DateListPlot[ WeatherData["Munich", "MeanTemperature", {{2010, 1, 1}, {2010, 12, 31}, "Day"}], Joined -> True]
ermittelt den Verlauf der durchschnittlichen Tagestemperaturen für München für das Jahr 2010.
Um etwa die Niederschlagsmengen in Boston für die Jahre 2010 bis 2020 in einem Diagramm darzustellen, das geht so:
DateListPlot[ WeatherData["KBOS","TotalPrecipitation", {{2010, 1, 1}, {2020, 12, 31}, "Month"}],Joined -> True]
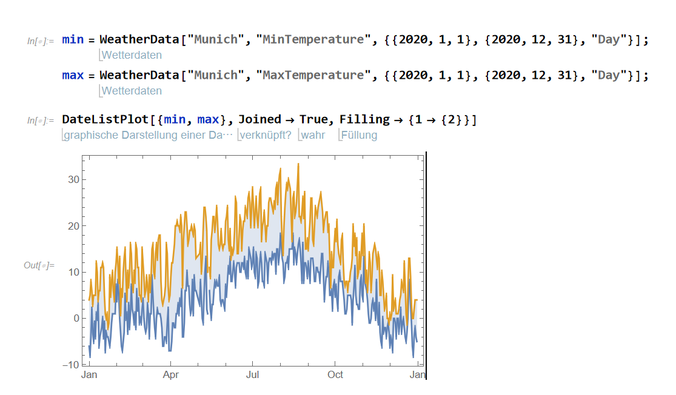
Ein abschließendes Beispiel zeigt den Verlauf der Tageshöchst- und Tiefsttemperaturen eines beliebigen Jahres. Dazu geben Sie nacheinander die folgenden drei Zeilen ein und evaluieren sie.
min = WeatherData["Munich", "MinTemperature", {{2020, 1, 1}, {2020, 12, 31}, "Day"}];
max = WeatherData["Munich", "MaxTemperature", {{2020, 1, 1}, {2020, 12, 31}, "Day"}];
DateListPlot[{min, max}, Joined -> True, Filling -> {1 -> {2}}]
Das Semikolon am Ende bewirkt, dass die Ausgabe unterdrückt wird.
Chemie: Elemente und Moleküle
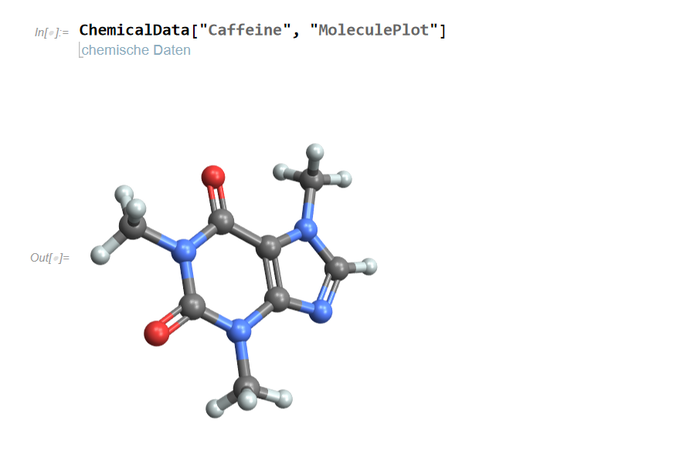
Mathematica kennt Tausende chemische Moleküle und unzählige Detailinformationen dazu. Passionierte Kaffeetrinker haben sich vielleicht schon einmal gefragt, wie die entscheidende Substanz, das Koffein, eigentlich aussieht. Mathematica kann diese Frage beantworten mit ChemicalData["Caffeine", "MoleculePlot"]. Das Molekül ist frei drehbar, was auf dem Raspberry Pi allerdings etwas ruckelt. Wer stattdessen das Strukturmodell bevorzugt, holt sich dies mit ChemicalData["Caffeine", "StructureGraph"] auf den Schirm.
Aminosäuren sind die Bestandteile von Proteinen und kommen in allen Lebewesen vor. Der folgende Code erstellt eine übersichtliche Tabelle mit allen Aminosäuren samt Strukturmodell und Summenformel:
GraphicsGrid[ EntityValue[ EntityClass["Chemical", "AminoAcids"], {"ColorStructureDiagram", "Formula", "Name"}], ImageSize -> 500, Frame -> All]
Eine Ebene darunter bei den Elementen kommt ein anderer Datensatz zum Einsatz. Um etwa das häufigste Element Wasserstoff unter die Lupe zu nehmen, verwendet man den Befehl ElementData["Hydrogen", "AtomicNumber"]. Die Ordnungszahl von Wasserstoff ist 1. Wasserstoff schmilzt bei frostigen Temperaturen. Der genaue Schmelzpunkt lässt sich mit ElementData["Hydrogen", "MeltingPoint"] ermitteln und der Siedepunkt mit ElementData["Hydrogen", "BoilingPoint"].
Gold ist deswegen so wertvoll, weil es selten ist. Wie selten, enthüllt der Befehl ElementData["Gold", "UniverseAbundance"]. Das Ergebnis: 1 Gramm Universum enthält 6*10^-10 Gramm Gold – oder anders gesagt, von 60 Milliarden Teilchen ist eins aus Gold.
Anatomie: Nerven und Knochen
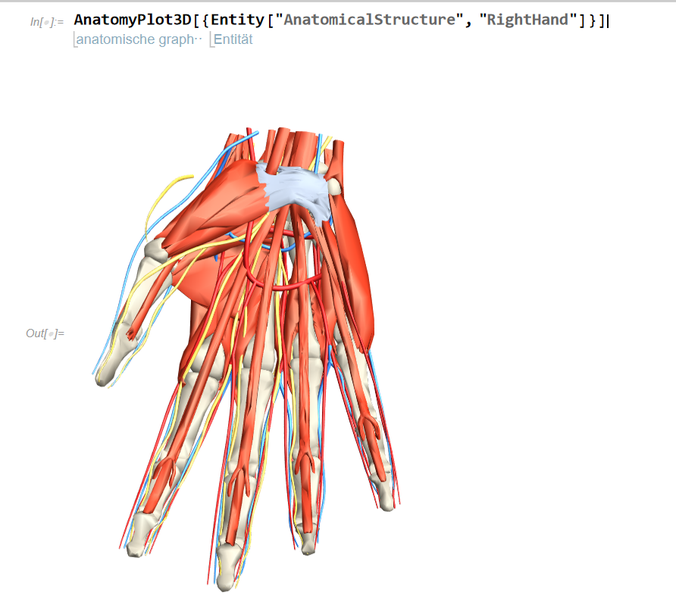
Mathematica kennt knapp 100.000 anatomische Daten. Um einzelne Knochen zu visualisieren, sollte man den Fachbegriff in Englisch kennen. Der Oberschenkelknochen etwa nennt sich Femur. Um also den linken Oberschenkelknochen darzustellen, kann man im Mathematica AnatomyPlot3D[Entity["AnatomicalStructure", "LeftFemur"]] eingeben. Die rechte Hand mit allem, was dazugehört, erhält man mit AnatomyPlot3D[{Entity["AnatomicalStructure", "RightHand"]}] und das Herz mit AnatomyPlot3D[{Entity["AnatomicalStructure", "Heart"]}].
Der Informationsgehalt und die Darstellung lässt sich mit Themes variieren. Das wissenschaftliche Theme zeigt die meisten Details und versieht sie mit erklärenden Tooltips: AnatomyPlot3D[{Entity["AnatomicalStructure", "Heart"]}, PlotTheme -> "Scientific"].
Um sich auf die Knochen zu konzentrieren, stehen wie so häufig bei Mathematica mehrere Wege offen. Einer davon sieht so aus:
Entity["AnatomicalStructure", "Skull"]["Graphics3D"] /. Annotation[x_, y_] :> Tooltip[x, y["Name"]]
Das Ergebnis ist ein Schädel, der mit Hilfe von Tooltips anzeigt, wie der Knochen heißt, der sich gerade unter dem Mauszeiger befindet.
Linguistik: Wortwolken und Übersetzungen
Mathematica ist polyglott. Das Programm enthält Wortlisten in vielen Sprachen. Um die zehn längsten deutschen Wörter in der Wortliste zu finden, geben Sie Folgendes ein: TakeLargestBy[WordList[Language -> "German"], StringLength, 10]. Einzelne Wörter lassen sich in der Art WordTranslation["hello", "French"] übersetzen. Nach der Eingabe von WordTranslation["hello", "Japanese"] erhält man japanische Schriftzeichen, die sich mit Transliterate[WordTranslation["hello", "Japanese"]] in eine für Europäer lesbare Form verwandeln lassen. Mathematica kann auch die Bedeutung von Wörtern erklären. Mal angenommen, Sie wollen wissen, was eigentlich ein Billabong ist, dann geben Sie einfach WordDefinition["billabong"] ein. Und wer sich schon Mal gefragt hat, wie ein arabisches Tastaturlayout aussieht, der bekommt mit LanguageData[Entity["Language", "Arabic"], "KeyboardImage"] eine Antwort.
Um Schwerpunkte in Texten zu erkennen, kann man Wortwolken erstellen. Je häufiger ein Wort vorkommt, desto größer erscheint es. Als Beispiel dient die Wikipedia-Seite zum Thema Mathematica. Eine Wortwolke lässt sich daraus erstellen mit WordCloud[WikipediaData["Mathematica"]].
Mathematik: Zahlen und Funktionen
Mathematica kann natürlich auch Mathematik. Die internen Funktionen sind auf Geschwindigkeit optimiert und liefern die Ergebnisse mit einer beliebigen Genauigkeit. Um etwa die 1000. Primzahl zu ermitteln, gibt man lediglich Prime[1000] ein und erhält als Ergebnis 7919. Eine Liste der ersten 100 Primzahlen liefert Table[Prime[n], {n, 100}]. Eine grafische Darstellung mit ListPlot[Table[Callout[Prime[n], Prime[n]], {n, 50}]] zeigt, dass zwischen 113 und 127 eine große Lücke klafft.
Wer sich mit Geometrie beschäftigt, kommt an der Zahl Pi kaum vorbei. Mathematica berechnet mühelos die ersten 1000 Stellen mit N[Pi, 1000]. Etwas aufwendiger sind die Fibonacci-Zahlen. Sie hängen mit dem Goldenen Schnitt zusammen und beginnen mit zwei Einsern, danach ergibt jeweils die Summe zweier aufeinanderfolgender Zahlen die folgende Zahl, also 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 und so weiter. Die rekursive Berechnung der Fibonacci-Zahlen ist recht kompliziert, aber Mathematica hat auch dafür eine eingebaute Funktion. Table[Fibonacci[n], {n, 25}] listet die ersten 25 Fibonacci-Zahlen auf. Man erkennt, dass diese schnell anwachsen. Fibonacci[1000] //Timing ermittelt die tausendste Fibonacci-Zahl und benötigt dafür weniger als eine tausendstel Sekunde. Das Verhältnis aufeinanderfolgender Fibonacci-Zahlen nähert sich dem Goldenen Schnitt an: Fibonacci[1000]/Fibonacci[999] // N ergibt 1,61803.
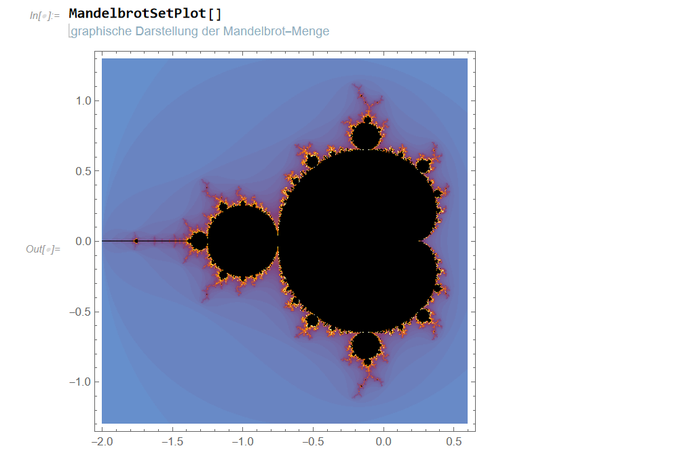
Wer früher einen C64 besaß, hat womöglich nächtelang fraktale Apfelmännchen berechnet, ein anderer Name für die Mandelbrot-Menge. Mit Mathematica geht das deutlich schneller. Ein einfaches MandelbrotSetPlot[] genügt. Interessant wird es aber erst, wenn man in die fraktalen Tiefen hinuntertaucht. Ausgehend von
MandelbrotSetPlot[{-0.68 + 0.48 I, -0.4 + 0.72 I}, MaxIterations -> 200, ColorFunction -> "RedBlueTones"]
lassen sich die Werte variieren und so immer neue Muster entdecken, die wahrscheinlich noch niemand je zuvor gesehen hat.
MandelbrotSetPlot[{-0.743 + 0.175 I, -0.723 + 0.195 I}, MaxIterations -> 800, ColorFunction -> "RedBlueTones"]
sieht schon völlig anders aus.
Alpha-Notebooks: Eingabe in natürlicher Sprache
Neben den standardmäßigen Notebook-Zellen verfügt Mathematica auch über Zellen, die direkt auf Wolfram Alpha [5] zugreifen. Das Besondere daran ist, dass sie natürliche englische Sprache verstehen und sogar Rechtschreibfehler verzeihen. Wenn Sie == eingeben, dann verwandelt sich das Eingabezeichen in einen Stern, um zu signalisieren, dass eine Abfrage von Wolfram Alpha folgt. Ist Kansas City die Hauptstadt von Kansas? Mit == capitals of the US states erhält man nicht nur eine Liste der Hauptstädte der 50 US-Staaten, sondern zusätzlich jede Menge weiterer Informationen.
Der Fantasie sind keine Grenzen gesetzt. Wie wäre es mit == distance to nearest star? Der nächstgelegene Stern ist natürlich die Sonne, aber zudem liefert das Programm eine Liste naher Sterne außerhalb des Sonnensystems. == number of languages in the world bringt ans Licht, dass es mehr als 7.000 lebende Sprachen auf der Erde gibt. Die Halbwertszeit von Uran 235 beträgt 704 Millionen Jahre, das ermittelt == half-life of uranium-235.
== population of iceland liefert neben vielen Zahlen und einer Bevölkerungspyramide auch die interessante Tatsache, dass auf dem Woodstock-Festival mehr Menschen waren als Island Einwohner hat.
Daten importieren und exportieren
Ein Import von Daten ist normalerweise nicht notwendig, da sich Mathematica alle benötigten Daten aus der Wolfram Cloud oder dem Knowledge Center holt oder falls nötig auch auf externe Quellen zugreift. Wenn Sie doch einmal Daten importieren wollen, dann funktioniert das nach dem Schema Import["C:\\Daten\\daten.xlsx"]. Mathematica versteht mehrere Hundert Dateiformate.
Um etwa Bilder aus einem Notebook auf die Festplatte zu speichern, klicken Sie es einfach an und wählen aus dem Kontextmenü „Save Graphic as…“. Das gesamte Notebook lässt sich über das File-Menü in ein anderes Format wie PDF exportieren. Um das Ganze programmatisch zu lösen, lässt sich etwa Export["primes.xls", Table[Prime[n], {n, 100}]] verwenden, um die ersten 100 Primzahlen im Excel-Format zu exportieren.
Weiterführende Informationen
Eine gute Anlaufstelle bei Fragen und Problemen ist das Documentation Center [6]. Über das Suchfeld gelangen Sie zu der gewünschten Funktion und erhalten ausführliche Informationen und Beispiele. Um die Wolfram Langue besser kennenzulernen, die Mathematica zugrunde liegt, steht ein ausführliches kostenloses E-Book zur Verfügung [7]. Stephen Wolfram hat „An Elementary Introduction to the Wolfram Language“ selbst geschrieben. In der Wolfrang Community [8] lassen sich Tipps und Anregungen abholen und Fragen stellen. Stack Exchange hat eine eigene Subdomain für Mathematica [9], die jedoch eher mathematisch ausgerichtet ist.
Unzählige Datensätze zum Ausprobieren und Experimentieren stellt das Wolfram Data Repository [10] bereit. Bei den meisten Datensätzen steht ein Notebook zum Download bereit, um damit direkt auf dem Raspberry Pi loszulegen.
Links und Quellen
[1] www.wolfram.com/language
[2] www.wolfram.com/raspberry-pi
[3] www.wolfram.com/knowledgebase
[4] www.world-airport-codes.com
[5] www.wolframalpha.com
[6] https://reference.wolfram.com
[7] www.wolfram.com/language/elementary-introduction
[8] https://community.wolfram.com
[9] https://mathematica.stackexchange.com
[10] https://datarepository.wolframcloud.com
 Schreiben macht durstig! Spendier mir doch ein Bier, indem du mir einen kleinen Betrag via Paypal schickst oder ein paar Bitcoin- oder Ethereum-Bruchteile an die entsprechende nachfolgende Adresse. Prost & auf dein Wohl!
Schreiben macht durstig! Spendier mir doch ein Bier, indem du mir einen kleinen Betrag via Paypal schickst oder ein paar Bitcoin- oder Ethereum-Bruchteile an die entsprechende nachfolgende Adresse. Prost & auf dein Wohl!
Bitcoin-Adresse : 1PjYNNjHmkAUmf626hukL32Vs1wFt8v1wT
Ethereum-Adresse : 0x974e73994c7483eef1396a21b9937aecb7b6c286

Schreibe einen Kommentar