Bitcoins verstehen

Bitcoins: Schlüssel, Adressen und Transaktionen

Mit Hilfe von ausgeklügelten mathematischen Operationen lassen sich aus privaten Schlüsseln öffentliche Schlüssel generieren und daraus wiederum Bitcoin-Adressen, die bei Transaktionen mit Bitcoins zum Einsatz kommen.
Bitcoins und Kryptowährungen sind ein Hype. Doch welche Mechanismen sich dahinter verbergen, welche Ideen für Sicherheit und Privatsphäre sorgen und wie Transaktionen im Detail ablaufen, bleibt meistens verborgen. Dieser Artikel erklärt die grundlegenden Schritte, die sich mit Hilfe von R und Python nachvollziehen lassen. Zwar gibt es mehrere Varianten und Notationen, aber im Wesentlichen ist die Vorgehensweise immer gleich.

Privater Schlüssel

Der Ausgangspunkt ist immer der Private Key. Er ist im Ergebnis eine zufällige 256-Bit-Zahl. Um einen privaten Schlüssel zu erzeugen, fügt man zunächst eine lange, zufällige Bitfolge zu einem String hinzu. Um mit sehr großen Zahlen umgehen zu können, ist das R-Package gmp nötig, das steht für „GNU Multiple Precision Arithmetic Library“. Das folgende R-Skript erzeugt die Bitfolge.

import(gmp)
n <- as.bigz("115792089237316195423570985008687907852837564279074904382605163141518161494337")
privkey <- "0b"
for(i in 1:500) {
  s <- toString(floor(runif(1, min=0, max=2)))
  privkey <- paste(privkey, s, collapse ="") }
privkey <- gsub(" ", "", privkey, fixed = TRUE)
privkey <- as.bigz(privkey)

Zwar erzeugt die Funktion runif() keine echten Zufallszahlen, sondern nur Pseudozufallszahlen, aber das soll für unsere Zwecke genügen. Die Variable n speichert den Grenzwert, ein privater Schlüssel darf nicht größer sein als diese Zahl. Die erzeugte 500-stellige Bitfolge lautet zum Beispiel: 0b1111111100101011101001111110000000010111010010100101100011110101
010111011100000111101010110111111001110001100000010101100001101111
010000110110000110100110101100100011000010000000011010011100100111
100110011011110100110010000011000110110000010010110001101000010111
000010001011010101100001101100110100001100000110101000111110100010
011101000100001010101000000000000010100001000011000100100111010101
010000001100010011001101011001011011010000111010111001111010000010
0100011110111111100000100001011111111111. Das vorangestellte 0b erleichtert die Umwandlung in eine Dezimalzahl mit der GMP-Funktion as.bigz. Zuvor werden noch die Leerzeichen entfernt. Die entsprechende Dezimalzahl lautet: 326278444287712137780482201259966177676698051670598392850673790601
967342552327427773633446453752045256554557775076412195961239795846
6490711682519799807. Aus dieser Zahl wird nun ein SHA256-Hash erzeugt, der in einer 256-Bit-Zahl resultiert. Dafür benötigt man das R-Package openssl und bindet es mit library(openssl) ein. Der Befehl privkey <- toString(sha256(privkey, key = NULL)) erzeugt dann den SHA256-Hash. Das Ergebnis wird üblicherweise als 64-stellige Hexadezimal angegeben: aed9028585c9b865604e4340c21cb33dd24638e5ac722508779d0214a09851f7. Die Zeilen privkey <- paste("0x", privkey) und privkey <- as.bigz(privkey) ergeben die Dezimalzahl, die kleiner als n sein muss, um einen validen privaten Schlüssel zu haben: 790858588698003789975129715825374475943960382396047228421659699788
94409290231. Vor den Gebrauch in Wallets erfolgt üblicherweise eine Umwandlung in das WIF-Format, zu erkennen an der 5 als erster Zahl. Dazu wird ein Base58-Check-Encoding durchgeführt. Das Alphabet von Base58 vermeidet Zweideutigkeiten wie 0 (Null) und O (großes o), I (großes i) und l (kleines L) und besteht aus 123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz. Da mir keine R-Library bekannt ist, die Base58 codieren kann, ein kurzer Ausflug zu Python. Die Library bitcoin enthält alle nötigen Funktionen:

import bitcoin
private_key = 0xaed9028585c9b865604e4340c21cb33dd24638e5ac722508779d0214a09851f7
wif_encoded_private_key = bitcoin.encode_privkey(decoded_private_key, 'wif')
print(wif_encoded_private_key)

ergibt 5K9HqAQsH8uJbojjDj4dcLR7ZWBPuMuamT4nxPu1no4yYKBTzKL als privaten Schlüssel im Wallet-Import-Format (WIF).

Öffentlicher Schlüssel

Der öffentliche Schlüssel wird aus dem privaten Schlüssel erzeugt. Hier wird es etwas mathematisch, denn dabei kommen elliptische Kurven zum Einsatz, bei Bitcoin ist dies die elliptische Kurve secp256k1. Sie folgt der Formel y^2 mod p = (x^3 + 7) mod p. Dabei ist mod der Modulo-Operator und p eine sehr große Primzahl: 2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1 oder 115792089237316195423570985008687907
853269984665640564039457584007908834671663. Dann kommt noch der Generator Point G ins Spiel. Er hat die Koordinaten (x, y) (55066263022277343669578
718895168534326250603453777594175500187360389116729240, 32670510020
758816978083085130507043184471273380659243275938904335757337482424) oder hexadezimal (04 79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2
815b16f81798, 483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08
ffb10d4b8). Kleiner Exkurs: Die Umwandlung einer sehr großen Zahl in eine Hexadezimalzahl erfolgt mit Hilfe des R-Packages Rmpfr:

library(Rmpfr)
x <- as.bigz("55066263022277343669578718895168534326250603453777594175500187360389116729240")
r <- formatMpfr(mpfr(x), base = 16, decimal.mark ="")
y <- as.bigz("32670510020758816978083085130507043184471273380659243275938904335757337482424")
s <- formatMpfr(mpfr(y), base = 16, decimal.mark ="")

Die Berechnung des öffentlichen Schlüssels erfolgt nach der Formel K = k * G. Dabei ist K der öffentliche Schlüssel, k der private Schlüssel und G der Generator Point. Da G auf der elliptischen Kurve liegt, ist auch K ein Punkt auf der Kurve und erfüllt die oben genannte Gleichung. Auch hier ist mir keine passende R-Funktion bekannt, die das berechnen könnte. Daher also wieder in Python:

import bitcoin
private_key = "aed9028585c9b865604e4340c21cb33dd24638e5ac722508779d0214a09851f7"
decoded_private_key = bitcoin.decode_privkey(private_key, 'hex')
public_key = bitcoin.fast_multiply(bitcoin.G, decoded_private_key)
print(public_key)

Das Ergebnis ist der Punkt (x,y) auf der elliptischen Kurve (44548637985885576293272528891886226804567452273278511865952833500212421414096, 31230969322060245064262007375378502447403080978162789446156741175970273815225). Das ist der öffentliche Schlüssel. Um statt Koordinaten eine Zahl zu erhalten, hängt man einfach den Y-Wert an den X-Wert an.
Für die weiteren Berechnungen benötigt man jedoch den öffentlichen Schlüssel im Hexadezimalformat. Dazu werden der X-Wert und der Y-Wert separat umgewandelt und dann aneinander gehängt. Das lässt sich mit einem kleinen R-Skript erledigen.

pubhex <- as.bigz("44548637985885576293272528891886226804567452273278511865952833500212421414096")
pubkeyhex_x <- formatMpfr(mpfr(pubhex), base = 16, decimal.mark ="")
pubhex <- as.bigz("31230969322060245064262007375378502447403080978162789446156741175970273815225")
pubkeyhex_y <- formatMpfr(mpfr(pubhex), base = 16, decimal.mark ="")
pubkeyhex <- paste("04", pubkeyhex_x, pubkeyhex_y, sep = "")
print(pubkeyhex)

Dem Ergebnis wird eine 04 vorangestellt, um anzuzeigen, dass es sich um einen unkomprimierten öffentlichen Schlüssel handelt. Zusammen ergibt das die Hex-Zahl 04627da2b4384e0a2e6a48416c0d2e50265e9939a0b33af1915ea6891137174cd0450
c1a2b035e78d6b53bfff20e1f500dd8dc43fd860283330177267698e9eab9.

Bitcoin-Adresse

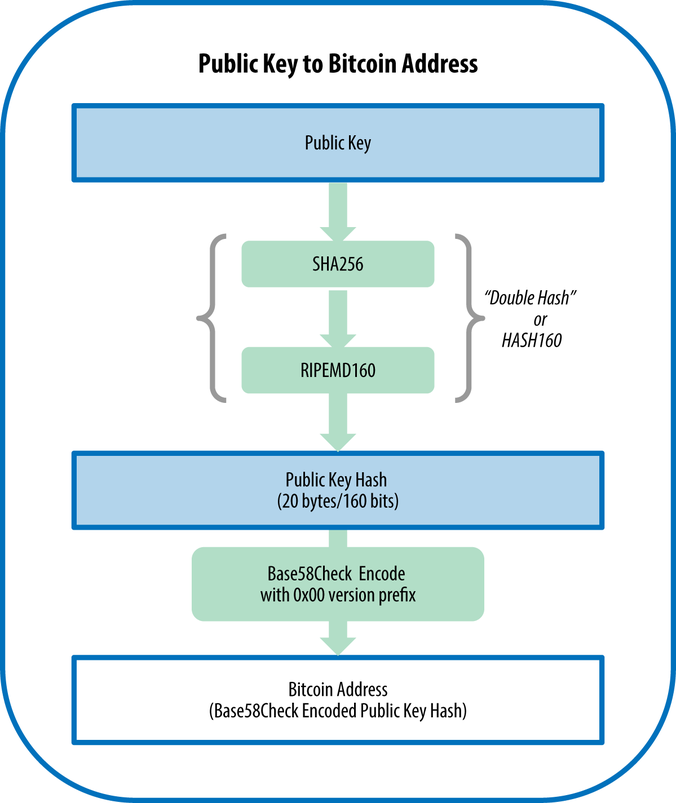
Um Bitcoins erwerben oder ausgeben zu können, ist eine Bitcoin-Adresse notwendig. Sie ist vergleichbar mit der IBAN bei SEPA-Überweisungen. Anders als der private Schlüssel muss sie nicht geheimgehalten werden. Die Bitcoin-Adresse lässt sich direkt aus dem öffentlichen Schlüssel erzeugen. Nachfolgend geht es um P2PKH, das Standardformat für Bitcoin-Adressen. P2PKH steht für "Pay To Public Key Hash" und bedeutet, dass man an den Hash eines öffentlichen Schlüssels bezahlt. Daneben gibt es noch P2SH-Adressen, "Pay to Script Hash". Dabei bezahlt man an den Hash eines Scripts. P2PKH-Adressen beginnen immer mit einer 1, P2SH-Adressen mit einer 3.
Die Erzeugung der Bitcoin-Adressen erfordert eine Reihe von Hashwert-Berechnungen. Diese müssen auf den öffentlichen Schlüssel im raw-Format angewendet werden und nicht auf die hexadezimale Darstellung. Dafür ist als zusätzliches Package wkb nötig. Der erste Schritt erzeugt einen SHA256-Hash des öffentlichen Schlüssels. Das lässt sich in R wiederum mit der Library openssl erledigen. Die Umwandlung in das raw-Format übernimmt die Funktion hex2raw().

library(gmp)
library(openssl)
pubkey <- as.bigz("04627da2b4384e0a2e6a48416c0d2e50265e9939a0b33af1915ea6891137174cd0450c1a2b035e78d6b53bfff20e1f500dd8dc43fd860283330177267698e9eab9")
hash1 <- toString(sha256(hex2raw(pubkeyhex), key = NULL))
print(hash1))

Zwischenergebnis: 29e9ec92371832186d555a675627a7932cd8fdc6d5b70a4736cf462e7de03b94. im zweiten Schritt erfolgt die Berechnung des Ripemd160-Hashes, ebenfalls auf das Raw-Format: hashnet <- toString(ripemd160(hex2raw(hash1))). Dem Ergebnis wird mit hashnet <- paste("00", hashnet, sep ="") eine 00 vorangestellt, was letztlich dazu führt, dass die Bitcoin-Adresse stets mit einer 1 beginnt. Das nächste Zwischenergebnis lautet 00353c0d31e95e5942691aeb6dd6529f2cd5a7b2ed.
Nun wird eine Checksumme berechnet, indem zweimal der Hash SHA256 auf das letzte Zwischenergebnis angewendet wird. Vom Ergebnis werden die ersten vier Byte bzw. acht Stellen genommen und an das vorherige Zwischenergebnis angehängt. Das nächste Zwischenergebnis: 00353c0d31e95e5942691aeb6dd6529f2cd5a7b2ed9a4ed060.

dcheck <- toString(sha256(hex2raw(hashnet)))
dcheck <- toString(sha256(hex2raw(dcheck)))
print(dcheck) #9a4ed06000d9457bd8cf46ceb3693572c1c68b16444d143b5642103354b11e38
checkadd <- paste(hashnet, "9a4ed060", sep ="")
print(checkadd)

Den abschließenden Schritt stellt eine Base58-Codierung dar. Diese erfolgt wieder in Python, wo eine Reihe Bibliotheken diese Codierung ermöglicht, etwa base58, die sich mit pip install base58 installieren lässt. Das Ergebnis ist eine frischgebackene Bitcoin-Adresse: 15rUkd3FBAt2995yGxBkw5FUgoLKudva8X.

import base58
hexstring= "00353c0d31e95e5942691aeb6dd6529f2cd5a7b2ed9a4ed060"
unencoded_string = bytes.fromhex(hexstring)
encoded_string= base58.b58encode(unencoded_string)
print(encoded_string)

Transaktionen

Transaktionen, also das Senden von Bitcoins von Sendern zu Empfängern, lassen sich am besten mit einem Blockchain-Explorer analysieren. Eine Transaktions-ID aus dem realen Leben: 63a9e0582ca3b51102c2f61cb2f5c2225e418e8d97ec4c4f1b2bb00c5242c9eb. Diese gibt man nun auf der Seite https://blockchain.info in das Suchfeld ein und erfährt zahlreiche Details. So ist die Transaktion in Block 507336 gespeichert. Zudem lassen sich Sender und Empfänger, Transaktionsgebühren und die Scripts ermitteln. Und über "Baum Chart anzeigen" lässt sich die Transaktion grafisch darstellen. Die Höhe der Transaktionsgebühren richtet sich nicht nach der Höhe des Bitcoin-Betrags, sondern nach der Größe, im Beispiel 339 Byte bei einer Gebühr von 165,566 Satoshi pro Byte.
1 Satoshi sind 0,00000001 Bitcoins.
Ein Block hat auch ein Gewicht, das in der Einheit Kilo Weight Units (KWU) angegeben ist. Das Gewicht hat mit dem Konzept Segregated Witness oder kurz segwit zu tun.
Ein weiterer Punkt: Bitcoins existieren nirgendwo, nicht auf der Festplatte und nicht im Wallet. Stattdessen gibt es Aufzeichnungen über Transaktionen zwischen verschiedenen Adressen mit Guthaben, die sich entweder erhöht oder verringert haben. Jede Transaktion, die jemals ausgeführt wurde, ist in der Blockchain gespeichert. Will man den Saldo einer Bitcoin-Adresse ermitteln, muss man diesen über die Blockchain errechnen, denn es werden keine Informationen in der Bitcoin-Adresse gespeichert.

Blockchain

Die Blockchain ist eine geordnete, rückverknüpfte Liste von Transaktionsblöcken. Die Blockchain kann als flache Datei oder in einer einfachen Datenbank gespeichert werden. Der Bitcoin Core Client speichert die Blockchain-Metadaten in der LevelDB-Datenbank von Google. Blöcke werden zurückverknüpft, wobei jeder Block auf den vorherigen Block in der Kette verweist. Die Blockkette wird oft als vertikaler Stapel visualisiert, wobei die Blöcke übereinander geschichtet sind. Die Visualisierung von übereinander gestapelten Blöcken führt zur Verwendung von Begriffen wie "height" für den Abstand vom ersten Block und "top" oder "tip" für den zuletzt hinzugefügten Block. Jeder Block innerhalb der Blockkette wird durch einen Hash identifiziert, der mit dem kryptographischen Hash-Algorithmus SHA256 auf den Header des Blocks erzeugt wird. Jeder Block referenziert auch einen vorhergehenden Block, den so genannten Parent-Block, über das Feld "previous block hash" im Blockkopf. Mit anderen Worten, jeder Block enthält den Hash des übergeordneten Blocks in seinem eigenen Header. Die Abfolge der Hashes, die jeden Block mit seinem Elternteil verbinden, erzeugt eine Kette, die bis zum ersten jemals erstellten Block, dem Genesis-Block, zurückreicht. Eine Änderung in einem Block hätte zwingend Änderungen in allen nachfolgenden Blöcken zur Folge.
Das Ziel von Mining ist nicht die Erschaffung neuer Bitcoins, sondern die Verifizierung neuer Blöcke, die dann an die Blockchain angehängt werden. Zur Belohnung für diesen Vorgang erhält der Miner derzeit als Belohnung 12,5 Bitcoins plus die in dem verifizierten und hinzugefügten Block enthaltenen Transaktionsgebühren. Ein solcher Block wird etwa alle 10 Minuten zur Blockchain hinzugefügt und kann mehrere hundert Transaktionen enthalten. Pro Tag haben Miner also 144 Chancen, Bitcoins zu erhalten. Jedoch halbiert sich die Belohnung alle paar Jahre, während die Schwierigkeit der Berechnungen immer weiter zunimmt.
Der Proof-of-Work-Algorithmus, den ein Miner lösen muss, besteht darin, einen "Nonce" genannten Wert zu finden, so dass der SHA256-Bit-Hash des Blockheader kleiner ist als ein Target- oder Zielwert. der im Block selbst als "Target Bits" oder nur "Bits" angegeben ist. Je kleiner das Target, desto schwieriger ist es, einen passenden Nonce-Wert zu finden. Vergleichbar ist das mit einem Wurf von zwei Würfeln: Eine Summe von 11 oder niedriger ist leicht zu erreichen, eine Summe von 3 oder niedriger hingegen nicht. Aus dem Target lässt sich der Wert errechnen, den der SHA256-Hash des Headers unterschreiten muss:

Beispiel: Block 512656
Target Bits = 391481763
Hexwert des Target Bits = 175589a3
Exponent = 17, coefficient = 5589a3
Berechnung des Schwellenwerts: target = coefficient * 2^(8 * (exponent – 3))
also: 0x5589a3 * 2^(0x08 * (0x17 - 0x03))
entspricht: 0x5589a3 * 2^(0x08 * (0x14))
entspricht: 0x5589a3 * 2^A0
Dezimal: 5605795 * 2^160
Ergebnis: 8192878571041388924351625416816775770172128369752145920
Ergebnis in Hex: 0000000000000000005589a30000000000000000000000000000000000000000
# Dieser 64-stellige Wert muss beim ebenfalls 64-stelligen SHA256-Hash des Headers unterschritten werden.
# Dazu müssen viele Millarden Nonce-Werte ausprobiert werden.

Wer Englisch kann und tiefer in die Materie einsteigen will, dem sei das hervorragende Buch "Mastering Bitcoin: Unlocking Digital Cryptocurrencies" von Andreas Antonopoulos empfohlen.

Schreiben macht durstig! Spendier mir doch ein Bier, indem du mir einen kleinen Betrag via Paypal schickst oder ein paar Bitcoin- oder Ethereum-Bruchteile an die entsprechende nachfolgende Adresse. Prost & auf dein Wohl!

Bitcoin-Adresse : 1PjYNNjHmkAUmf626hukL32Vs1wFt8v1wT
Ethereum-Adresse : 0x974e73994c7483eef1396a21b9937aecb7b6c286